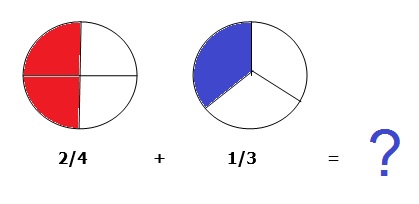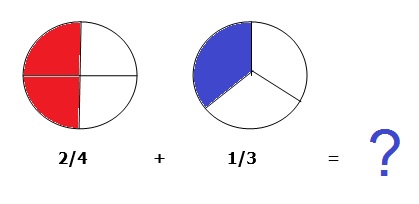CONTEÚDOS E METODOLOGIAS DO ENSINO DE MATEMÁTICA
Segundo o PCN de Matemática, um dos critérios de avaliação de para o segundo ciclo é: ler, escrever números naturais e racionais, ordenar números naturais e racionais na forma decimal, pela interpretação do valor posicional de cada uma das ordens.
Ao raciocinar sobre os números racionais como se fossem naturais, os alunos acabam tendo que enfrentar vários obstáculos. Analise-os abaixo e classifique-os em verdadeiro (V) ou falso (F).
( ) um deles está ligado ao fato de que cada número racional pode ser representado por diferentes (e infinitas) escritas fracionárias; por exemplo, 1/3, 2/6, 3/9 e 4/12 são diferentes representações de um mesmo número.
( ) outro diz respeito à comparação entre racionais: acostumados com a relação 3 > 2, terão que construir uma escrita que lhes parece contraditória, ou seja, 1/3 < 1/2.
( ) se o “tamanho” da escrita numérica era um bom indicador da ordem de grandeza no caso dos números naturais (8.345 > 41), a comparação entre 2,3 e 2,125 já não obedece ao mesmo critério.
( ) se ao multiplicar um número natural por outro natural (sendo este diferente de 0 ou 1) a expectativa era a de encontrar um número maior que ambos, ao multiplicar 10 por 1/2 se surpreenderão ao ver que o resultado é menor do que 10.
( ) se a sequência dos números naturais permite falar em sucessor e antecessor, para os racionais isso não faz sentido, uma vez que entre dois números racionais quaisquer é sempre possível encontrar outro racional; assim, o aluno deverá perceber que entre 0,8 e 0,9 estão números como 0,81, 0,815 ou 0,87.
É correto o que se afirma em:
V, V, F, F, V
V, V, V, F, F
V, V, F, V, V
V, V, V, V, V
V, F, V, F, V
Da mesma forma que podemos realizar operações de adição, subtração, multiplicação e divisão com os números naturais, também, podemos realizar essas operações com os números fracionários. O diferencial das operações envolvendo frações consiste na peculiaridade de cada fração e operação.
I- Para somarmos ou subtrairmos frações com o mesmo denominador, devemos conservar o denominador e subtrair ou somar o numerador.
II- Para somarmos ou subtrairmos frações com denominadores diferentes, precisamos encontrar frações equivalentes que tenham o mesmo denominador.
III- Para resolver a fração de um número inteiro basta dividir o número pelo denominador, e o resultado multiplicar pelo numerador.
IV- Para resolver a multiplicação de fração por fração deve-se multiplicar numerador com numerador e denominador com denominador.
V- Para resolver uma divisão de frações, devemos copiar a primeira fração, trocar o sinal da divisão para multiplicação e inverter a segunda fração.
É correto apenas o que se afirma em
I, III e V apenas.
I, II, III, IV e V.
I, III, IV e V apenas.
I, II, IV e V apenas.
II, III, IV e V apenas.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.
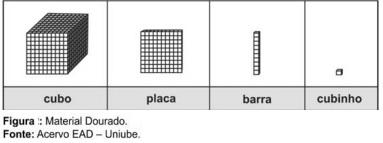
Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, F, V, V, V
V, V, F, F, V
V, V, V, V, V
V, V, F, V, F
V, V, V, F, F
Em uma olimpíada na universidade foram distribuídas 18 medalhas para futebol de salão e 12 medalhas para queimada. O time da turma de Pedagogia jogou futebol e ganhou 11 das 18 medalhas. E o time da turma de Letras ganhou 9 das 12 medalhas.
Com base nestas informações quais as frações que representam as medalhas que cada um dos times ganharam?
Assinale a única alternativa correta.
Pedagogia (18/12) e Letras (11/9)
Pedagogia (18/11) e Letras (12/9)
Pedagogia (7/3) e Letras (12/18)
Pedagogia (7/18) e Letras (3/12)
Pedagogia (11/18) e Letras (9/12)
Fração própria, fração imprópria, fração equivalente, fração mista e fração aparente são nomenclaturas dadas aos diferentes tipos de fração. E para determinar cada uma delas compara-se os valores do numerador com os do denominador.
Com base nesta afirmação analise os valores do numerador e do denominador de cada fração, em seguida numere a segunda coluna de acordo com a primeira.
- 5/7 ( ) Fração imprópria
- 2/3 e 8/12 ( ) Fração aparente
- 7/3 ( ) Fração própria
- 7 /7 ( ) Frações equivalentes
- 3 2/4 ( ) Fração mista
Assinale a sequencia correta.
3, 5, 1 , 2, 4
4, 3, 2, 1, 5
3, 4, 1 , 2, 5
4, 3, 1, 2, 5
3, 1, 4 , 2, 5
- A palavra múltiplo vem de multiplicação. Numa multiplicação, o produto (resultado da multiplicação) é sempre múltiplo de cada um dos fatores. Para encontramos o conjunto de múltiplos de um número, basta multiplicá-lo pela sucessão de números naturais. O conjunto dos múltiplos de um número natural é infinito.
- Divisores de qualquer número natural, são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero. O conjunto dos divisores de um número é um conjunto finito.
Leia e analise as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a alternativa que apresenta a sequencia correta.
- Os múltiplos de 11 menores que 70 são: 11, 22, 33, 44, 55.
- Os divisores de 11 são 1 e ele mesmo. Dessa forma 11 é um número primo.
- O maior divisor comum entre 24 e 9 é: 3.
- O menor múltiplo comum entre 5 e 12 é: 60.
- Os números 1, 2, 3, 5, 7 são primos menores que 10.
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
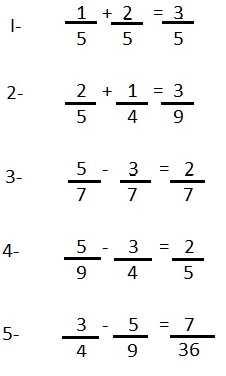
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
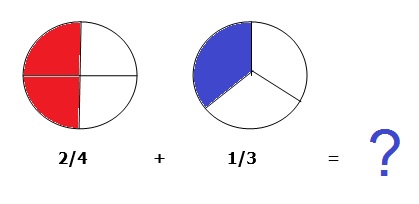
V, V, F, F, V
V, V, V, F, F
V, V, F, V, V
V, V, V, V, V
V, F, V, F, V
Da mesma forma que podemos realizar operações de adição, subtração, multiplicação e divisão com os números naturais, também, podemos realizar essas operações com os números fracionários. O diferencial das operações envolvendo frações consiste na peculiaridade de cada fração e operação.
I- Para somarmos ou subtrairmos frações com o mesmo denominador, devemos conservar o denominador e subtrair ou somar o numerador.
II- Para somarmos ou subtrairmos frações com denominadores diferentes, precisamos encontrar frações equivalentes que tenham o mesmo denominador.
III- Para resolver a fração de um número inteiro basta dividir o número pelo denominador, e o resultado multiplicar pelo numerador.
IV- Para resolver a multiplicação de fração por fração deve-se multiplicar numerador com numerador e denominador com denominador.
V- Para resolver uma divisão de frações, devemos copiar a primeira fração, trocar o sinal da divisão para multiplicação e inverter a segunda fração.
É correto apenas o que se afirma em
I, III e V apenas.
I, II, III, IV e V.
I, III, IV e V apenas.
I, II, IV e V apenas.
II, III, IV e V apenas.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, F, V, V, V
V, V, F, F, V
V, V, V, V, V
V, V, F, V, F
V, V, V, F, F
Em uma olimpíada na universidade foram distribuídas 18 medalhas para futebol de salão e 12 medalhas para queimada. O time da turma de Pedagogia jogou futebol e ganhou 11 das 18 medalhas. E o time da turma de Letras ganhou 9 das 12 medalhas.
Com base nestas informações quais as frações que representam as medalhas que cada um dos times ganharam?
Assinale a única alternativa correta.
Pedagogia (18/12) e Letras (11/9)
Pedagogia (18/11) e Letras (12/9)
Pedagogia (7/3) e Letras (12/18)
Pedagogia (7/18) e Letras (3/12)
Pedagogia (11/18) e Letras (9/12)
Fração própria, fração imprópria, fração equivalente, fração mista e fração aparente são nomenclaturas dadas aos diferentes tipos de fração. E para determinar cada uma delas compara-se os valores do numerador com os do denominador.
Com base nesta afirmação analise os valores do numerador e do denominador de cada fração, em seguida numere a segunda coluna de acordo com a primeira.
- 5/7 ( ) Fração imprópria
- 2/3 e 8/12 ( ) Fração aparente
- 7/3 ( ) Fração própria
- 7 /7 ( ) Frações equivalentes
- 3 2/4 ( ) Fração mista
Assinale a sequencia correta.
3, 5, 1 , 2, 4
4, 3, 2, 1, 5
3, 4, 1 , 2, 5
4, 3, 1, 2, 5
3, 1, 4 , 2, 5
- A palavra múltiplo vem de multiplicação. Numa multiplicação, o produto (resultado da multiplicação) é sempre múltiplo de cada um dos fatores. Para encontramos o conjunto de múltiplos de um número, basta multiplicá-lo pela sucessão de números naturais. O conjunto dos múltiplos de um número natural é infinito.
- Divisores de qualquer número natural, são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero. O conjunto dos divisores de um número é um conjunto finito.
Leia e analise as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a alternativa que apresenta a sequencia correta.
- Os múltiplos de 11 menores que 70 são: 11, 22, 33, 44, 55.
- Os divisores de 11 são 1 e ele mesmo. Dessa forma 11 é um número primo.
- O maior divisor comum entre 24 e 9 é: 3.
- O menor múltiplo comum entre 5 e 12 é: 60.
- Os números 1, 2, 3, 5, 7 são primos menores que 10.
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
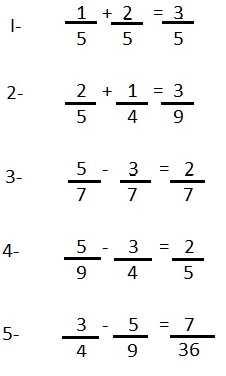
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
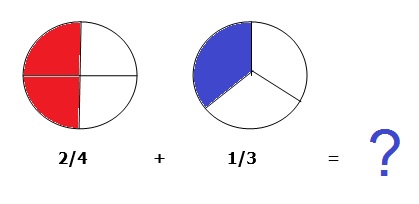
I, III e V apenas.
I, II, III, IV e V.
I, III, IV e V apenas.
I, II, IV e V apenas.
II, III, IV e V apenas.
“No que se refere a Matemática, no primeiro ciclo as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática.
Os conhecimentos das crianças não estão classificados em campos (numéricos, geométricos, métricos, etc.), mas sim interligados. Essa forma articulada deve ser preservada no trabalho do professor, pois as crianças terão melhores condições de apreender o significado dos diferentes conteúdos se conseguirem perceber diferentes relações deles entre si.
Desse modo, embora o professor tenha os blocos de conteúdo como referência para seu trabalho, ele deve apresentá-los aos alunos da forma mais integrada possível.
Em função da própria diversidade das experiências vivenciadas pelas crianças também não é possível definir, de forma única, uma sequência em que conteúdos matemáticos serão trabalhados nem mesmo o nível de aprofundamento que lhes será dado.
Por outro lado, o trabalho a ser desenvolvido não pode ser improvisado, pois há objetivos a serem atingidos. Embora seja possível e aconselhável que em cada sala de aula sejam percorridos diferentes caminhos, é importante que o professor tenha coordenadas orientadoras do seu trabalho; os objetivos e os blocos de conteúdos são excelentes guias”. (Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.p.44 ).
Os estudos realizados acerca da aprendizagem pelas crianças, nos levou a entender que as mesmas aprendem pela ação. Assim, podemos afirmar que a manipulação, a exploração de materiais concretos possibilita o trabalho com números. E o Material Dourado auxilia na construção do conceito de número e as suas operações, geometria bem como na álgebra. Nesta atividade exploraremos esse recurso para representar os números na base 10.

Com base neste entendimento leia e analise as alternativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a sequencia correta.
- O material dourado recebe este nome por ser feito por contas douradas, foi criado pela médica educadora Maria Montessori para atender a crianças com deficiência mental.
- O material dourado é composto por cubinhos que representam as unidades, por barrinhas subdivididas em dez partes iguais; que representam as dezenas, por placas subdivididas em cem cubinhos ou dez barrinhas que representam as centenas, e por um cubo grande; que representa a unidade de milhar.
- Com o material dourado podemos relacionar número e quantidade, as quatro operações, o cálculo de área, volume.
- O trabalho com material dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
- No material dourado cada dez cubinhos correspondem a dez unidades e podemos trocar por uma barrinha (dezena), cada dez barrinhas equivalem a 100 unidades podem ser trocadas por uma placa (centena), e cada dez placas que equivalem a uma milhar podemos trocar pelo ao cubo maior, que representa a milhar.
V, F, V, V, V
V, V, F, F, V
V, V, V, V, V
V, V, F, V, F
V, V, V, F, F
Em uma olimpíada na universidade foram distribuídas 18 medalhas para futebol de salão e 12 medalhas para queimada. O time da turma de Pedagogia jogou futebol e ganhou 11 das 18 medalhas. E o time da turma de Letras ganhou 9 das 12 medalhas.
Com base nestas informações quais as frações que representam as medalhas que cada um dos times ganharam?
Assinale a única alternativa correta.
Pedagogia (18/12) e Letras (11/9)
Pedagogia (18/11) e Letras (12/9)
Pedagogia (7/3) e Letras (12/18)
Pedagogia (7/18) e Letras (3/12)
Pedagogia (11/18) e Letras (9/12)
Fração própria, fração imprópria, fração equivalente, fração mista e fração aparente são nomenclaturas dadas aos diferentes tipos de fração. E para determinar cada uma delas compara-se os valores do numerador com os do denominador.
Com base nesta afirmação analise os valores do numerador e do denominador de cada fração, em seguida numere a segunda coluna de acordo com a primeira.
- 5/7 ( ) Fração imprópria
- 2/3 e 8/12 ( ) Fração aparente
- 7/3 ( ) Fração própria
- 7 /7 ( ) Frações equivalentes
- 3 2/4 ( ) Fração mista
Assinale a sequencia correta.
3, 5, 1 , 2, 4
4, 3, 2, 1, 5
3, 4, 1 , 2, 5
4, 3, 1, 2, 5
3, 1, 4 , 2, 5
- A palavra múltiplo vem de multiplicação. Numa multiplicação, o produto (resultado da multiplicação) é sempre múltiplo de cada um dos fatores. Para encontramos o conjunto de múltiplos de um número, basta multiplicá-lo pela sucessão de números naturais. O conjunto dos múltiplos de um número natural é infinito.
- Divisores de qualquer número natural, são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero. O conjunto dos divisores de um número é um conjunto finito.
Leia e analise as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a alternativa que apresenta a sequencia correta.
- Os múltiplos de 11 menores que 70 são: 11, 22, 33, 44, 55.
- Os divisores de 11 são 1 e ele mesmo. Dessa forma 11 é um número primo.
- O maior divisor comum entre 24 e 9 é: 3.
- O menor múltiplo comum entre 5 e 12 é: 60.
- Os números 1, 2, 3, 5, 7 são primos menores que 10.
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
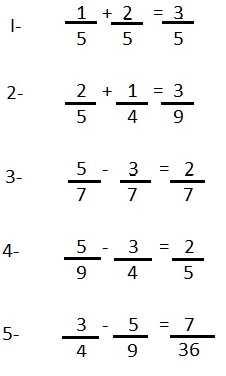
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
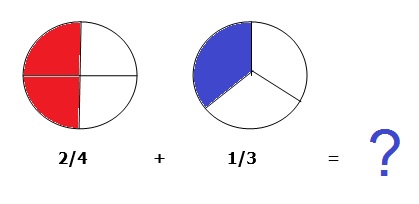

V, F, V, V, V
V, V, F, F, V
V, V, V, V, V
V, V, F, V, F
V, V, V, F, F
Em uma olimpíada na universidade foram distribuídas 18 medalhas para futebol de salão e 12 medalhas para queimada. O time da turma de Pedagogia jogou futebol e ganhou 11 das 18 medalhas. E o time da turma de Letras ganhou 9 das 12 medalhas.
Com base nestas informações quais as frações que representam as medalhas que cada um dos times ganharam?
Assinale a única alternativa correta.
Pedagogia (18/12) e Letras (11/9)
Pedagogia (18/11) e Letras (12/9)
Pedagogia (7/3) e Letras (12/18)
Pedagogia (7/18) e Letras (3/12)
Pedagogia (11/18) e Letras (9/12)
Fração própria, fração imprópria, fração equivalente, fração mista e fração aparente são nomenclaturas dadas aos diferentes tipos de fração. E para determinar cada uma delas compara-se os valores do numerador com os do denominador.
Com base nesta afirmação analise os valores do numerador e do denominador de cada fração, em seguida numere a segunda coluna de acordo com a primeira.
- 5/7 ( ) Fração imprópria
- 2/3 e 8/12 ( ) Fração aparente
- 7/3 ( ) Fração própria
- 7 /7 ( ) Frações equivalentes
- 3 2/4 ( ) Fração mista
Assinale a sequencia correta.
3, 5, 1 , 2, 4
4, 3, 2, 1, 5
3, 4, 1 , 2, 5
4, 3, 1, 2, 5
3, 1, 4 , 2, 5
- A palavra múltiplo vem de multiplicação. Numa multiplicação, o produto (resultado da multiplicação) é sempre múltiplo de cada um dos fatores. Para encontramos o conjunto de múltiplos de um número, basta multiplicá-lo pela sucessão de números naturais. O conjunto dos múltiplos de um número natural é infinito.
- Divisores de qualquer número natural, são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero. O conjunto dos divisores de um número é um conjunto finito.
Leia e analise as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a alternativa que apresenta a sequencia correta.
- Os múltiplos de 11 menores que 70 são: 11, 22, 33, 44, 55.
- Os divisores de 11 são 1 e ele mesmo. Dessa forma 11 é um número primo.
- O maior divisor comum entre 24 e 9 é: 3.
- O menor múltiplo comum entre 5 e 12 é: 60.
- Os números 1, 2, 3, 5, 7 são primos menores que 10.
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
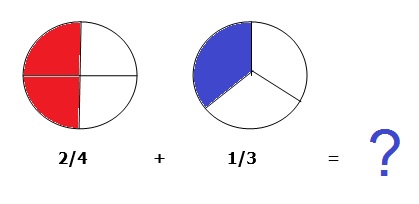
Pedagogia (18/12) e Letras (11/9)
Pedagogia (18/11) e Letras (12/9)
Pedagogia (7/3) e Letras (12/18)
Pedagogia (7/18) e Letras (3/12)
Pedagogia (11/18) e Letras (9/12)
Fração própria, fração imprópria, fração equivalente, fração mista e fração aparente são nomenclaturas dadas aos diferentes tipos de fração. E para determinar cada uma delas compara-se os valores do numerador com os do denominador.
Com base nesta afirmação analise os valores do numerador e do denominador de cada fração, em seguida numere a segunda coluna de acordo com a primeira.
- 5/7 ( ) Fração imprópria
- 2/3 e 8/12 ( ) Fração aparente
- 7/3 ( ) Fração própria
- 7 /7 ( ) Frações equivalentes
- 3 2/4 ( ) Fração mista
Assinale a sequencia correta.
3, 5, 1 , 2, 4
4, 3, 2, 1, 5
3, 4, 1 , 2, 5
4, 3, 1, 2, 5
3, 1, 4 , 2, 5
- A palavra múltiplo vem de multiplicação. Numa multiplicação, o produto (resultado da multiplicação) é sempre múltiplo de cada um dos fatores. Para encontramos o conjunto de múltiplos de um número, basta multiplicá-lo pela sucessão de números naturais. O conjunto dos múltiplos de um número natural é infinito.
- Divisores de qualquer número natural, são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero. O conjunto dos divisores de um número é um conjunto finito.
Leia e analise as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a alternativa que apresenta a sequencia correta.
- Os múltiplos de 11 menores que 70 são: 11, 22, 33, 44, 55.
- Os divisores de 11 são 1 e ele mesmo. Dessa forma 11 é um número primo.
- O maior divisor comum entre 24 e 9 é: 3.
- O menor múltiplo comum entre 5 e 12 é: 60.
- Os números 1, 2, 3, 5, 7 são primos menores que 10.
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
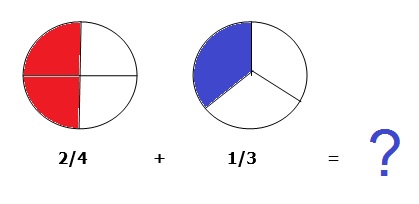
3, 5, 1 , 2, 4
4, 3, 2, 1, 5
3, 4, 1 , 2, 5
4, 3, 1, 2, 5
3, 1, 4 , 2, 5
- A palavra múltiplo vem de multiplicação. Numa multiplicação, o produto (resultado da multiplicação) é sempre múltiplo de cada um dos fatores. Para encontramos o conjunto de múltiplos de um número, basta multiplicá-lo pela sucessão de números naturais. O conjunto dos múltiplos de um número natural é infinito.
- Divisores de qualquer número natural, são todos os números naturais que ao dividirem tal número, resultarão em uma divisão exata, isto é, com resto igual a zero. O conjunto dos divisores de um número é um conjunto finito.
Leia e analise as afirmativas abaixo e classifique em verdadeiras ou falsas. Em seguida assinale a alternativa que apresenta a sequencia correta.
- Os múltiplos de 11 menores que 70 são: 11, 22, 33, 44, 55.
- Os divisores de 11 são 1 e ele mesmo. Dessa forma 11 é um número primo.
- O maior divisor comum entre 24 e 9 é: 3.
- O menor múltiplo comum entre 5 e 12 é: 60.
- Os números 1, 2, 3, 5, 7 são primos menores que 10.
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
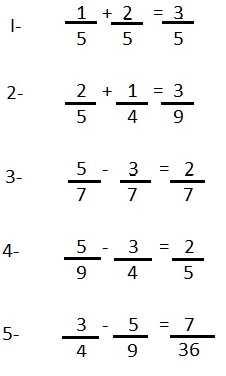
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
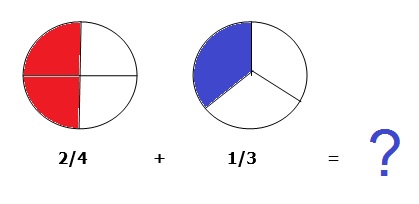
V, V, V, V, F.
F, V, V, V, V.
V, V, V, V, V.
F, V, V, V, F.
F, F, V, V, F.
Uma figura geométrica é plana, quando todos os seus pontos estiverem em um mesmo plano, ou seja, a figura plana é apenas representada por desenhos, não conseguimos pegá-la.

Sobre este estudo temos que:
- Um quadrado é uma figura geométrica plana.
- Um cubo é uma figura geométrica plana.
- Um paralelepípedo é uma figura geométrica plana.
- Um triangulo é uma figura geométrica plana.
- Uma retângulo é uma figura geométrica plana.
Assinale a alternativa com a sequência correta
V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
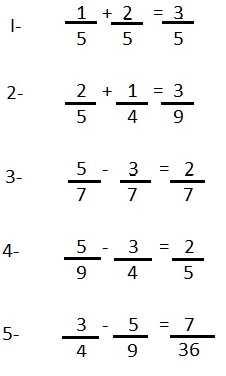
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
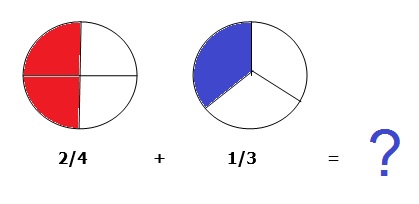

V, V, F, F, V
V, F, V, V, F
V, V, F, V, F
V, F, F, V, F
V, F, F, V, V
As operações aritméticas
A palavra aritmética deriva da palavra grega arithmos, que significa número. A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se possam realizar sobre esses números, nos diferentes conjuntos numéricos. (CENTURIÓN, Marília. Números e operações. p.88,1995.)
É comum uma criança ao tentar resolver um problema, perguntar: “a operação é de ‘mais’ ou de ‘menos’?”, é para multiplicar ou dividir? Perguntas como estas comprovam que a criança não conseguiu identificar no problema as ideias envolvidas e não associou logicamente a essas operações as operações a serem realizadas.
Isso posto, o domínio do sistema de numeração decimal é imprescindível para compreensão dos algoritmos das operações em N. Com base nesta afirmação assinale a alternativa errada.
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
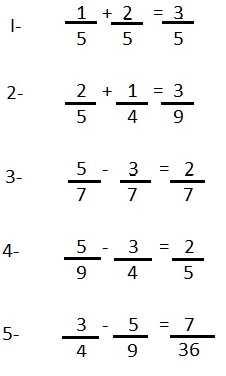
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
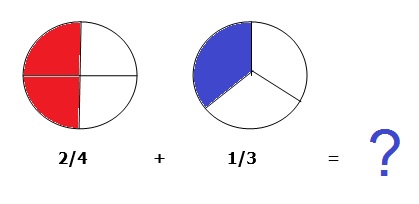
Associativa (2 x 4) x 3 ou 2 x (4 x 3), elemento neutro 1 x 3 = 3 x 1, comutativa 5 x 2 = 2 x 5, fechamento 4 x 6 =24 e distributiva 2 x (2 + 3) = 2 x 2 + 2 x 3 , são propriedades da multiplicação.
A multiplicação é a soma de parcelas iguais. “No primeiro ano, entre as atividades de adição, devem ser incluídas adição com mais de duas parcelas e também com parcelas iguais.” (ROSA, Ernesto, Didática da Matemática. p.110, 2010.)
A operação da subtração em N envolve três idéias: de retirar; comparar e aditiva de completar. A pergunta: “ Com quantos vai ficar?” está relacionada a ideia de completar. Podemos comparar quantidades perguntando: “Quanto uma tem a mais que a outra?” E para comparar temos uma pergunta como:”Quantos (o) a mais?”. A ideia de retirar nos remete a pergunta: “ Quanto deverá adquirir para ficar com a mesma quantidade que eu?”.
A operação de adição está ligada a situações que envolvem as ações de reunir ou juntar e de acrescentar. Para a ideia de reunir ou juntar, temos a pergunta: quantos ao todo? Na ideia de acrescentar o aluno encontrará pergunta como: Com quantas vai ou vão ficar?
O termo “vai um” significa o transporte de uma ordem para a ordem imediatamente superior, que significa “vai uma dezena, uma centena, uma milhar” e, assim, sucessivamente para as ordens seguintes.
A adição, subtração, multiplicação e divisão são operações básicas da matemática. Assim, como nos números naturais, essas operações podem ser realizadas com os números racionais. As regras para somar frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração.
Sobre a soma e subtração de frações temos:
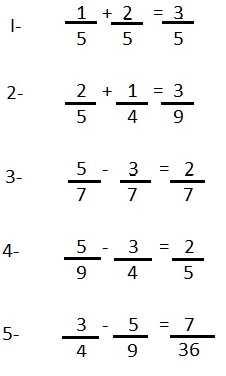
É correto o que se afirma em:
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.
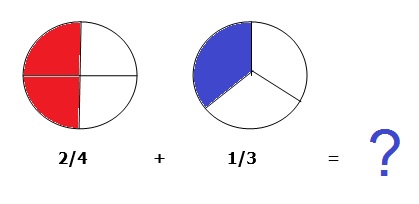
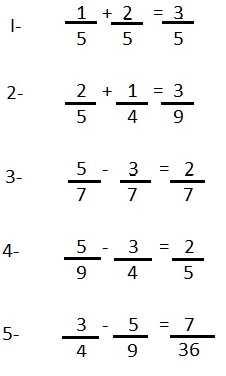
V, F, V, V, V
V, V, F, F, V
F, V, F, V, F
V, F, V, F, V
V, F, V, F, F
A soma ou adição de frações requer que todas as frações envolvidas possuam o mesmo denominador. Com base nesta afirmação analise as imagens abaixo em seguida resolva a operação indicada e assinale a alternativa com a resposta correta.
Obs. A resposta não está simplificada.